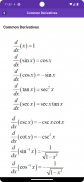
Calculus Formulas

Matematik, 'sürekli değişim' araştırmasına ve denklem çözme uygulamalarına katılır. İki ana dalı vardır:

1: değişim oranları ve eğrilerin eğimi ile ilgili olan Diferansiyel Hesap .

2: miktarların ve eğrilerin altındaki ve alanların birikimi ile ilgili İntegral Hesaplama .

Hem Diferansiyel Analizler hem de İntegral Analizler, sonsuz dizilerin ve sonsuz serilerin yakınsaklık kavramlarını iyi tanımlanmış bir limite dönüştürür. Bu iki dal, hesabın temel teoremi ile ilgilidir.

Diferansiyel Matematik, değişim oranını hesaplamak için bir alanı küçük parçalara böler. İntegral hesap, alanı veya hacmi hesaplamak için küçük parçalara katılır. Kısacası, muhakeme ya da hesaplama yöntemidir.

Bu uygulamada, integral formülü, türev formülü, limit formülü vb gibi Analiz Formüllerinin bir listesini görebilirsiniz.

Sınır Formülleri şunları içerir:

Limit Tanımları.

Limit ve tek taraflı limitler arasındaki ilişki.

Sınırlayıcı Özellikler Formülleri.

Temel Limit Değerlendirme Formülleri.

Değerlendirme Teknikleri Formüller.

Bazı Sürekli Fonksiyonlar.

Ara Değer Teoremi.

Herhangi bir Matematik Sınırını çözün.

Türev Formüllerinde:

Türevlerin Tanımı ve Notasyonu.

Türevin Yorumlanması.

Temel Özellikler ve Formüller.

Ortak türevler.

Zincir Kuralı Değişkenleri.

Yüksek Mertebeden Türevler.

Örtük Farklılaşma.

Artırma / Azaltma - İçbükey Yukarı / İçbükey Aşağı.

Extrema.

Ortalama değer teoremi.

Newton’un Yöntemi.

İlgili Fiyatlar

Optimizasyon

Integrals Formüllerinde şunlar bulunur:

İntegral tanımları.

Analizin Temel Teoremi.

Özellikleri.

Ortak İntegraller.

Standart Entegrasyon Teknikleri.

Yanlış İntegral.

Belirli İntegrallere Yaklaşım.

Matematik öğrencileri için çok kullanışlı bir uygulama.